一张空白的格子图,加上几组简单的数字,就能“织”出各式像素图片?这似乎听起来有些不可思议,但已经在全世界风靡20余年,尤其在日本较为流行,国内通常翻译为数织。
数织的历史
数织是诞生于上世纪八十年代末的绘图游戏,由日本人西尾彻也(にしお てつや,日本著名谜题工作者)与石田(いしだのん,全名不详,维基上Non Ishida为错误翻译)各自独立发现,石田的相关作品在周日电讯报(The Sunday Telegraph)上发表时被James Dalgety 称为Nonograms(ののぐらむ),此后逐渐在全球范围普及开来。值得一提的是,虽然这款游戏在中国知名度不算高,但在日本还是有一定知名度,Jupiter Corporation在任天堂多部世代机(包括GBA、3DS、ns等)上都发布过数织游戏,其最新作Picross S8在2022年9月29日登录Switch平台。
基础规则
1、谜面
数织谜题和数独等游戏相似,都是格子谜题,每道谜题包括一张n*n的空白格子表,在每列格子最左边和每行最上面都有一组(或一个)数字,玩家可以根据这张谜题判断每个格子画圈或画叉,当所有空格都填满后,画圈的格子就能构成唯一的设计好的图形。
2、数的含义
2.1 单个数
在谜面最左边和最上边的数是解开数织的唯一线索。以单个数来说,数字n代表所在的行/列有n个挨在一起的格子被涂黑,例如下图为已解出的谜题,第一行没有填充,第二行有三个相邻填充,第三行没有填充;对应每一列刚好都有一个填充。

再比如稍微复杂一点的情况,如下
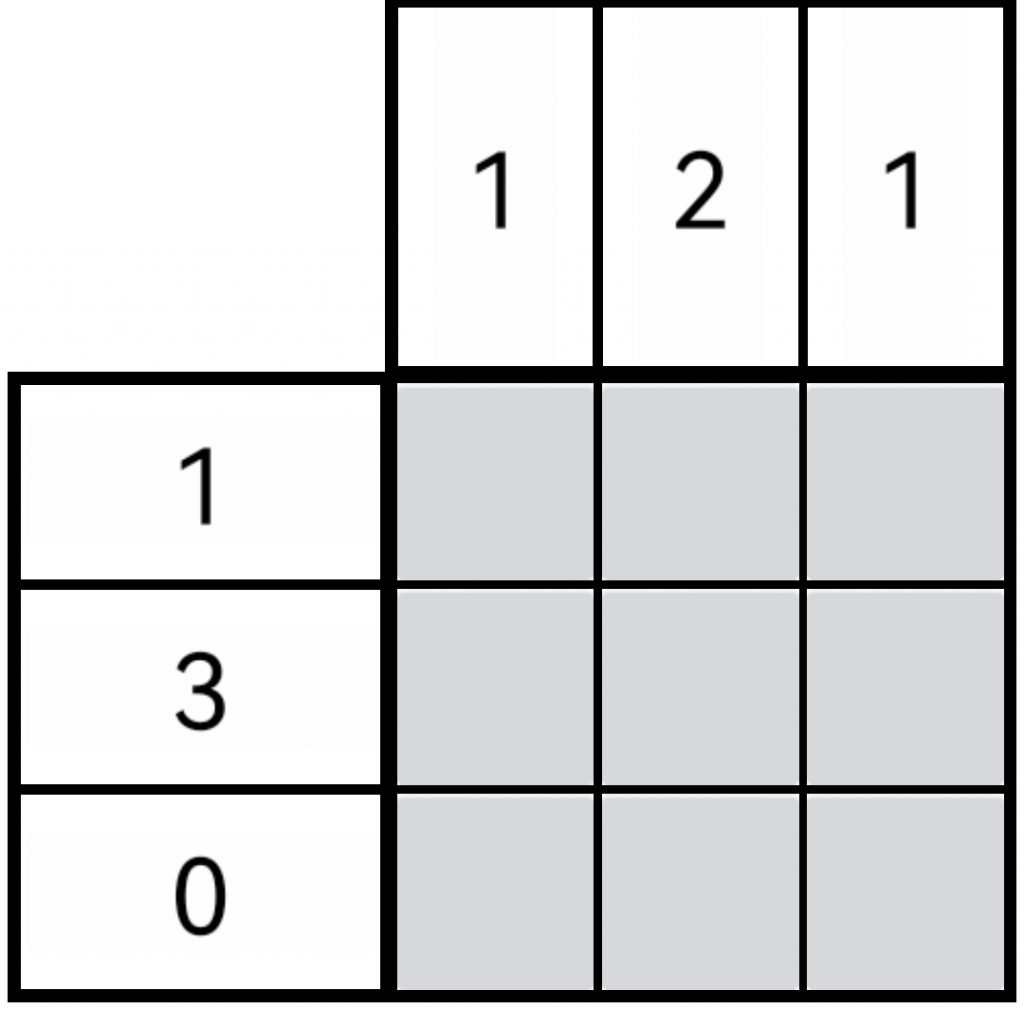
可以观察到第二行三个全满,填入后第一列与第三列都刚好满足数量,如下(绿色表示行、列满足个数要求)

剩余第二列需要修改,根据第一行与第二列信息可以推测,填入中间偏上的格子。

2.2多个数
复杂图形不可能保证所有涂色的方块都紧靠在一起,因此可以用多个数描述复杂的情况。例如(5,4)表示改行/列有两块紧挨在一起的空格被涂色,而且严格按照从左到右/从上到下的顺序,分别是5个格子和4个格子,而且这两个涂色条之间的未涂色格子数可以为任意值。例如在一个1*14的格子里,(5,4)可以表示以下情况(未完全列举)



3、检查
按照行与列的数字规则进行涂黑(为起到辅助功能,可以在确认的不涂黑的格子处画叉,完成后擦除),进行对照检查,保证每行、每列都满足对应的要求,即视为完成谜题。
实战技巧
(本部分建议先适当练习,并至少完成一张9*9的谜题后再阅读)
数织的谜面有不同规格,图案越简单、行列数越少则谜题越简单,其独特的规则保证了每个正确的谜面对映唯一的一幅图像,也能衍生出许多技巧。比如一个大佬将这些特点转换成了数学化、逻辑化的语言。这里综合自身游玩经验加以总结,以通俗化的语言进行分析(以下例子均是以10*10的谜面为例子):
1、固定排列。拿到谜面后,应当仔细观察每一行列的数字,可能存在行或列,只可能有一种排列方式。例如(10)表明本行/列全部填黑,(6 3)表明本行/列只可能为6黑1白3黑的排列方式,如果再隐蔽一点可能不容易发现,比如(2 2 1 2)也只有一种固定排列,为2黑1白2黑1白1黑1白2黑。如果先找到这种固定排列可以获得相当丰富的信息,但是许多复杂谜题都不存在这种固定排列。
2、限制排列。试想,(6 3)是固定的排列,那(6 2)就一定一点信息都无法获得吗?不妨列出所有可能性的图像



可以发现,从左起第2-6个、第9个格子都是一定会涂黑的,如下

这也就给我们启发,在特殊情况下某些组合的格子可以被部分地确定。以总格子数为b、侧边数字为(a)为例,用(b-a)相当于涂色条可以运动的自由度,如果a>(b-a)时,说明涂色条不是“完全自由的”,肯定有一部分必被涂黑,涂黑的块数为a-(b-a)=2a-b,且坐落于总格子正中间。例如某行/列为(8),则自由度为2,8-2=6,则正中间6格必被涂黑。
以总格子数为c、侧边数组为(a b)的情况为例,自由度的计算式类推为[c-(b+a+1)](有1是因为两个涂黑条之间必定至少有一个空格),然后分别用自由度与a、b进行比较(为什么不和a+b+1比较呢?因为a与b之间并非一定是1个空白格,因此这两部分也相对可能可以运动),确定好固定格子数后,分别从左(、右)扣除自由度等量的格子数后,即可按照数量从左(右)确定必定涂黑的格子。例如对上面的进行验证,10个格子,侧面数组为(6 2),则自由度为10-6-1-2=1,6>1,2>1,两边均有固定涂黑的部分,则空掉最左边和最右边两格子,分别依次涂黑5个和1个格子,,发现完美与上面吻合。再举例练习,若数组为(5 1)时,自由度为10-5-1-1=3,5>3,1<3,仅有左边有固定涂黑的部分,即空余3格涂黑两格。
当数组的数字多于两组时也可类推,不再做多余推导说明。
3、更新格子信息。当利用上述技巧和基本推导方法获得部分线索后,应当适时重新观察其它未知行列,进一步获得新的信息。例如原有某行为(5),自由度也为5,则没有固定涂黑的部分。但若已推导出第2列、第10列信息后得知第2格、第10格必定不涂黑,如下

由于5个格子必定连续涂黑,则第一格也必定不涂黑。那么重新观察本行,可以发现可填涂的总格子数就变成7格了,自由度变成2,那必有三个格子会被涂黑,如下图

然后又可以根据列信息对第5-7列进行推导,更新新的格子信息。
4、切入口。一般来说,在没有固定排列的情况下,从角落开始尝试是最优选择,而且选择之间有差异。因为假设某个角落涂黑,则可以同时开始推断一行、一列的信息,由于处于角落,因此自由度被限制,涂黑的顺序只有一个方向,有利于推导出更多信息,并且正是这个特点,最好从长数端进行假设。通俗地举个例子,第一行为(3 1),那么如果是假设左上角涂黑,则可以得知1-3格均涂黑,但如果是假设右上角涂黑,就只能得到一格的信息。但是并非每一题都可以从角落开始推断。笔者援引两个可行方法:1、根据对称性判断尝试(例如第1、10行分别为(1 2)(2 1),第1、10列分别为(2 1)(1 2));2、没有固定排列时,选择自由度较低的行列下手。
除了以上技巧以外,数织还有众多技巧、经验,例如假设法、(1 1 1 1)特殊法等等,笔者仅列举其中较为重要和有趣的部分分享,欢迎读者自行尝试总结。
例题(nonograms应用 10*10困难-3):

本题的关键点在四个角,以及第1、5、6、10四列。
首先观察到图片应该是轴对称图,这对我们的解题至关重要。然后先分别尝试四个角,发现都不可能涂黑,否则推导有误。四个角画叉后更新各自信息,发现1、10两列自由度缩减,出现必涂黑的四个格子,可以更新为下图。

然后可以发现第2行最右端与3有关,又毗邻两个涂色方块,不妨假设其涂色,进行推断,发现推断到如下图后又需要分类讨论,会比较复杂,之后可以再讨论2行1列的格子涂黑与不涂黑,也是能够推断出均矛盾。

另一种更优的方法是假设第2行最右端格子不涂黑,因为涂黑的话第10列仍存在两种可能,但如果不涂黑的话第10列的格子信息可以固定,可以直接连续推断出答案。

数织的意义:
数织的魅力在于,解开谜题就好像纺织一般,需要找到一个破题口,然后横竖交错,抽丝剥茧,不断通过线索获得新的信息,加以整合后转化成新的线索进行下一轮解题。但是它的意义仅限于此吗?
一张像素为100*100的图片进行传输需要多少数据量?如果是按照位图传输、不考虑传输协议带来的额外开销、按照rgb编码需要100000个int32,即总共是400k的字节。那如果将图片转化成数织的数字形式进行传输,会消耗多少数据?一个100*100像素的数织包含200组数,平均来说每组数个数都在10个以下,每个数基本都是一位数或者二位数,在每组数前增加一个修饰数描述组内数字个数(因为个数不可知),即大致数据量基本都小于200*10*4=800个int32,但由于picross远远使用不到整个int32的范围,因此如果不考虑压缩、明文储存的话最优应该是少于800个字节,大大节约了数据传输的成本。那么试想,如果可以编程程序,较快将数织信息转化成图片信息,那么就可以通过(图片转化数字)——(数字传输)——(数字转化图片)的形式进行低成本传输。
虽然这种方法听起来非常诱人,但初步分析有两个技术上的难题:一是以上的讨论都是针对picorss,即像素点少的情况,当像素个数过多时,程序能否顺利解出图片还不得而知(这种理想技术本身可以看作以算力赚成本);另外如今基本上都传输彩色图片,那么许多渐变部分虽然都涂色,但需要额外修饰,因此这种理想化的传输模型只能针对黑白像素图片,甚至不适用于灰度图片。虽然笔者不是从事计算机和美术专业,但大胆提出一个优化方法:首先通过叠加的方法解决灰度,即一张黑白的灰度图片可以通过10张泾渭分明的像素图象模拟(打个比方,这样可以区分10级灰度),那么也就是说原有基础10倍数据量就能解决这个问题(但是算力需求也要10倍);再说色彩问题,一个彩色图片可以通过三原色的色彩通道综合形成,每个色彩通道对应一张灰度图,那么再在之前的基础上翻三倍即可。也就是说,一张100*100的像素图数据少于24k的字节,并且无论图片大小,总共需要处理数字转化图片的次数都是30次。因为本身对编程和绘图了解较少,所以这种方法是否有前景、10级灰度是否够用等都不得而知,如果真能有所研究发现,烦请转我点技术股份(笑)。
总结
总的来说,相较于数独等游戏来说,数织寿命尚年轻,且似乎更有些实用的意味在里面,休闲时间不妨一试亦是乐事。(初学者推荐app应用“以数织图Nonogram”,但是会有无时长限制的广告弹窗)



0 条评论